| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- DFS
- querySelector
- 230503
- intent
- classList
- 생명주기
- 프래그먼트
- 안드로이드
- ActionBar
- null-safety
- html
- 230510
- C++
- Adapter
- 함수 인자
- parcelable
- DOMContentLoaded
- Flutter
- javascript
- 230508
- string
- Class
- putextra
- textContent
- fragment
- 데이터 타입
- serializable
- 부가데이터
- ViewPager
- 인텐트
- Today
- Total
나만의 개발노트
[알고리즘] 탐색 알고리즘 - DFS, BFS 본문
---키워드---
1. 깊이 우선 탐색 (DFS)
2. 너비 우선 탐색 (BFS)
* 정점(node) = N
간선(edge) = E
그래프를 탐색한다 = 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것.
1. 깊이 우선 탐색 (DFS, Depth-First Search)
: 최대한 깊이 내려간 뒤, 더이상 갈 곳이 없을 경우 옆으로 이동
| 깊이 우선 탐색(DFS, Depth-First Search) | 너비 우선 탐색(BFS, Breath-First Search) |
| :최대한 깊이 내려간 뒤, 더이상 갈 곳이 없을 경우 옆으로 이동 | : 최대한 넓게 이동한 다음, 더 이상 갈 수 없을 때 아래로 이동 |
| 1. 모든 노드를 방문하고자 하는 경우에 이 방법 2. 너비우선탐색(BFS)보다 좀 더 간단함 3. 검색 속도는 너비우선탐색(BFS)에 비해서 느림 |
1. 주로 두 노드 사이의 최단 경로를 찾고 싶을 때 이 방법 |
| 스택 또는 재귀함수로 구현 | 큐를 이용하여 구현 |
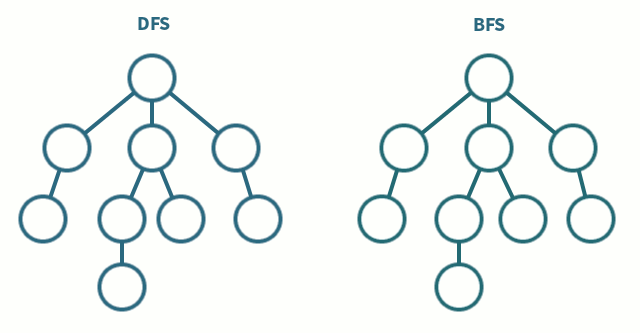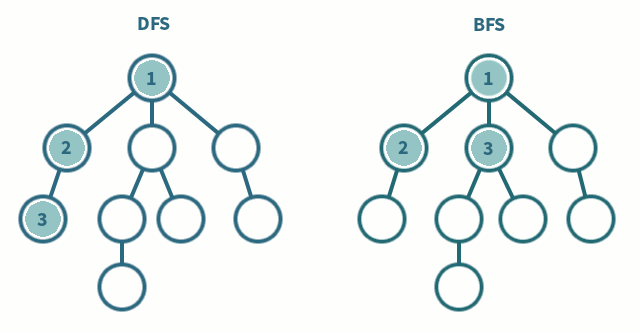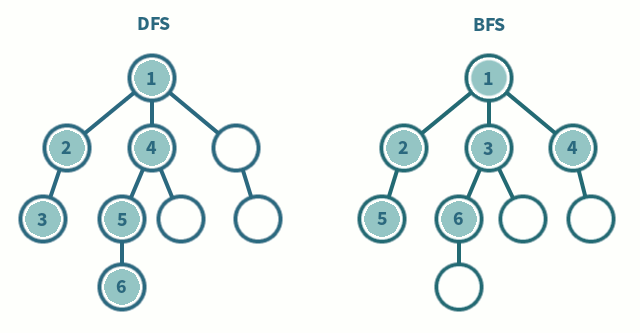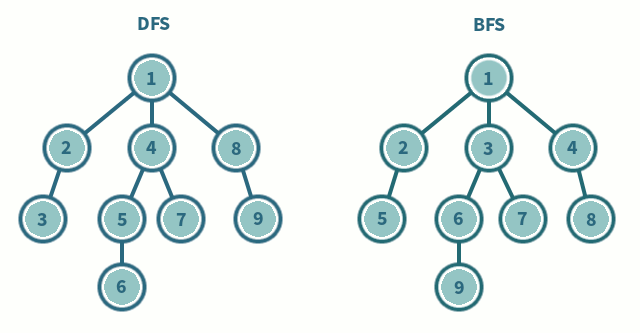
<인접리스트 VS 인접 행렬>
인접 리스트 : O(N+E)
인접 행렬 : O(N²)
일반적으로 E(간선)의 크기가 N²에 비해 상대적으로 적기 때문에
인접 리스트 방식이 효율적임
인접 행렬의 경우, 정점의 개수 N만큼 도는 2중 for문을 돌려 두 정점 간에 간선이 존재하는지를 확인해야 합니다.
이때 N의 제곱만큼 돌게 되므로 O(N²)의 시간 복잡도가 됩니다.
인접 리스트로 구현된 경우, 존재하는 간선의 정보만 저장되어 있으므로 인접 행렬에서 사용한 2중 for문이 필요하지 않습니다. 다음 노드가 방문하였는지 확인할 때 간선의 개수인 E의 두 배만큼의 시간이 걸리고(1번에서 2, 6번이 방문하였는지를 확인하고 2번에서 1,3,6번을 방문하였는지 확인합니다. 이때 1번과 2번의 간선 하나에 두 번의 확인을 하기 때문에 두배만큼 시간이 걸립니다.) 각 노드를 방문할 때 정점의 개수인 N만큼 걸립니다. 따라서 O(N+2*E) = O(N+E)가 됩니다. (시간 복잡도에서 계수는 삭제합니다.)
<DFS, BFS 활용한 문제 유형/응용>
1) 그래프의 모든 정점을 방문하는 것이 주요한 문제
= DFS, BFS 중 편한 것
2) 경로의 특징을 저장해둬야 하는 문제 (경로에 조건이 있는 경우)
= DFS
(* BFS는 경로의 특징을 가지지 못함)
3) 최단거리 구해야 하는 문제
= BFS 유리
왜냐하면 깊이 우선 탐색으로 경로를 검색할 경우 처음으로 발견되는 해답이 최단거리가 아닐 수 있지만,
너비 우선 탐색으로 현재 노드에서 가까운 곳부터 찾기 때문에경로를 탐색 시 먼저 찾아지는 해답이 곧 최단거리기 때문입니다.
4) 검색대상 그래프가 정말 크면, DFS 고려
검색 대상의 규모가 크지 않고, 검색 시작 지점으로부터 원하는 대상이 별로 멀지 않다면 BFS
<DFS와 BFS를 JAVA코드로>
1. DFS
1) 스택
2) 재귀함수 (더 보편적, 짧음)
2. BFS : 큐(Queue)
import java.util.*;
public class Num1260 {
static ArrayList<Integer>[] connections; //ArrayList<T>은 무엇
static boolean[] visited;
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int v = sc.nextInt();
connections = new ArrayList[n+1];
visited = new boolean[n+1];
for(int i=1;i<=n;i++){
connections[i] = new ArrayList<Integer>();
}
for(int i=0;i<m;i++){
int x = sc.nextInt();
int y = sc.nextInt();
connections[x].add(y);
connections[y].add(x);
}
for(int i=1;i<=n;i++){
Collections.sort(connections[i]); //Colletions 는 무엇인가
}
dfs(v);
Arrays.fill(visited,false); //Arrays.fill? visited 배열을 false로 초기화?
bfs(v);
}
public static void dfs(int Node){
System.out.print(Node + " ");
visited[Node] = true;
for(int i : connections[Node]){ //for 표기법?
if(visited[i]==false){
dfs(i);
}
}
System.out.println();
}
public static void bfs(int v){
Queue<Integer> queue = new LinkedList<Integer>(); //Queue<T> , LinkedList<T>
queue.add(v);
visited[v] = true;
while(!queue.isEmpty()){
int Node = queue.poll(); //queue.poll
System.out.print(Node + " ");
for(int i : connections[Node]){
if(visited[i] == false){
visited[i] = true;
queue.add(i);
}
}
}
}
}
'[알고리즘]' 카테고리의 다른 글
| [알고리즘] Backtracking (0) | 2024.06.05 |
|---|---|
| [알고리즘] DFS (0) | 2024.06.05 |
